Discrete Mathematics သည် Discrete Mathematics တွင် ပြီးပြည့်စုံသော သင်ယူမှုအတွေ့အကြုံကို ပံ့ပိုးပေးသည့် အသုံးပြုသူအတွက် အဆင်ပြေသောအက်ပ်တစ်ခုဖြစ်သည်။ ၎င်း၏ ကောင်းစွာဖွဲ့စည်းထားသော အခန်းငါးခန်းတွင် အက္ခရာသင်္ချာတည်ဆောက်ပုံများ၊ ဂရပ်သီအိုရီ၊ အုပ်စု homomorphism နှင့် isomorphism နှင့် propositional logic အပါအဝင် အဓိကအကြောင်းအရာများကို အကျုံးဝင်ပါသည်။ သန့်ရှင်းသော ဒီဇိုင်းသည် အာရုံထွေပြားမှုကို လျော့နည်းစေပြီး အသေးစိတ်ရှင်းပြချက်များ၊ ဂရပ်များ၊ ပုံကြမ်းများနှင့် သရုပ်ဖော်ပုံများသည် နားလည်မှုကို မြှင့်တင်ပေးပါသည်။ Discrete Mathematics သည် သီးခြားသင်္ချာကိုကျွမ်းကျင်စေရန်အတွက် အထိရောက်ဆုံးနှင့် လက်တွေ့ကျသောလမ်းကြောင်းကို ပေးဆောင်ပါသည်။ ယခုဒေါင်းလုဒ်လုပ်ပြီး သင်၏ ကြွယ်ဝသော သင်ယူမှုခရီးကို စတင်လိုက်ပါ။
အက်ပ် အင်္ဂါရပ်များ-
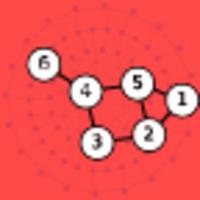
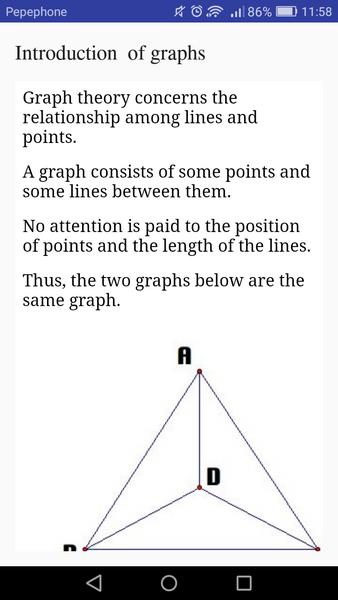
- ပြည့်စုံသောအကြောင်းအရာ- အက္ခရာသင်္ချာပုံသဏ္ဍာန်များ၊ ဂရပ်သီအိုရီ၊ အုပ်စု homomorphism နှင့် isomorphism နှင့် propositional logic အပါအဝင် ကျယ်ပြန့်သောသင်္ချာအကြောင်းအရာများပါရှိသော အခန်းငါးခန်း။ အလိုလိုသိနိုင်သောလမ်းကြောင်း-
- A ရိုးရှင်းပြီး အသုံးပြုရလွယ်ကူသော ဒီဇိုင်းသည် လွယ်ကူစွာ ရှာဖွေနိုင်ပြီး သီးခြားအကြောင်းအရာများကို ဝင်ရောက်ကြည့်ရှုနိုင်စေပါသည်။ ရှင်းလင်းသောရှင်းလင်းချက်များ-
- လေးနက်သောရှင်းပြချက်များကို ဂရပ်များ၊ ပုံများနှင့်လက်တွေ့ကျသောပုံများဖြင့် ပံ့ပိုးပေးထားပါသည်။ အနှောက်အယှက်ကင်းသော သင်ယူခြင်း-
- သန့်ရှင်းသပ်ရပ်သော အလှတရားသည် မလိုအပ်သော အာရုံထွေပြားမှုမရှိဘဲ အာရုံစူးစိုက်သင်ယူမှုကို သေချာစေသည်။ လက်တွေ့အသုံးချမှု-
- လက်တွေ့ကမ္ဘာနမူနာများနှင့် အပလီကေးရှင်းများသည် သီးခြားသင်္ချာသဘောတရားများ၏ ဆက်စပ်မှုနှင့် လက်တွေ့ကျမှုကို သရုပ်ဖော်သည်။ ထိရောက်သော သင်ယူခြင်းတူးလ်-
- အက်ပ်၏ ပြည့်စုံသော အကြောင်းအရာ၊ အလိုလိုသိနိုင်သည်။ လမ်းကြောင်းပြခြင်း၊ ရှင်းရှင်းလင်းလင်း ရှင်းပြချက်များနှင့် လက်တွေ့အသုံးချမှုများသည် အလွန်ထိရောက်သော သင်ကြားရေးကိရိယာတစ်ခု ဖြစ်လာစေသည်။ နိဂုံးချုပ်အနေနှင့်၊ Discrete Mathematics သည် Discrete Mathematics သင်ယူလိုသူတိုင်းအတွက် ထူးခြားသည့်အက်ပ်တစ်ခုဖြစ်သည်။ ၎င်း၏ ပြည့်စုံသော အကြောင်းအရာ၊ အသုံးပြုရလွယ်ကူသော ဒီဇိုင်း၊ ရှင်းရှင်းလင်းလင်း ရှင်းပြချက်များ၊ လက်တွေ့ကျသော အသုံးချပရိုဂရမ်များနှင့် အာရုံထွေပြားမှုကင်းသော ပတ်ဝန်းကျင်သည် ၎င်းအား တန်ဖိုးမဖြတ်နိုင်သော သင်ယူမှုရင်းမြစ်တစ်ခု ဖြစ်လာစေသည်။